Sætningen om den behårede kugle
I dagens artikel skal vi dykke ned i emnet Sætningen om den behårede kugle, som har skabt stor interesse i nutidens samfund. For at give et bredt og detaljeret overblik over dette emne, vil vi udforske forskellige aspekter relateret til Sætningen om den behårede kugle, fra dets oprindelse eller udvikling til dets indvirkning i forskellige sammenhænge. Igennem artiklen vil vi undersøge de forskellige perspektiver og meninger omkring Sætningen om den behårede kugle, samt de udfordringer og muligheder det giver. Ligeledes vil vi dykke ned i mulige løsninger eller strategier for at imødegå de vanskeligheder, der er forbundet med Sætningen om den behårede kugle. I sidste ende har denne artikel til formål at give læserne en dybere og mere fuldstændig forståelse af Sætningen om den behårede kugle, med det formål at opmuntre til dialog og refleksion over dette emne, der er så relevant i dag.
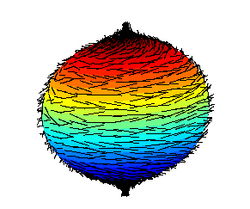

Sætningen om den behårede kugle er et resultat i algebraisk topologi, som siger, at ethvert kontinuert tangentvektorfelt på kugleoverfladen vil forsvinde i mindst et punkt: Hvis f er en kontinuert funktion fra 2-sfæren S2 til R3, så der i hvert punkt p på sfæren gælder, at f(p) er tangent til sfæren i p, så findes mindst et p, så f(p) = 0. Sætningen blev først formodet af Henri Poincaré sidst i 1800-tallet og første gang bevist af Brouwer i 1912.[1]
Sætningens navn skyldes, som illustrationerne viser, at resultatet giver, at "man ikke kan rede håret på en behåret kugle fladt uden at skabe et koslik". En generalisering af resultatet siger, at n-sfæren Sn har et kontinuert felt af tangentvektorer forskellige fra 0, hvis og kun hvis n er ulige.
En mærkværdig meteorologisk anvendelse af sætningen fremkommer ved betragtning af vindretning som en vektor defineret kontinuert over overfladen på en planet med atmosfære. Som en idealisering kan vind betragtes som en todimensional vektor, hvis dens ikke-tangentiale bevægelse er negligibel. I dette tilfælde siger sætningen, at der til ethvert tidspunkt eksisterer et punkt på planetoverfladen, hvor der er vindstille.
Fodnoter
- ^ "Arkiveret kopi". Arkiveret fra originalen 26. maj 2006. Hentet 25. marts 2009.