Omskrevet cirkel
Denne artikel vil tage fat på emnet Omskrevet cirkel, som har fået stor relevans i de senere år på grund af dets indflydelse på forskellige områder af samfundet. Gennem historien har Omskrevet cirkel været genstand for adskillige undersøgelser og debatter, hvilket har skabt stigende interesse fra akademikere, eksperter og den brede offentlighed. Denne artikel søger at analysere i dybden de mest relevante aspekter af Omskrevet cirkel, udforske dens mange dimensioner og dens indflydelse i forskellige sammenhænge. Ligeledes vil den seneste forskning relateret til Omskrevet cirkel blive undersøgt, for at give et komplet og opdateret syn på emnet. Gennem en kritisk og reflekterende tilgang er det hensigten at tilbyde læseren et berigende perspektiv, der bidrager til en større forståelse af Omskrevet cirkel og dets implikationer i nutidens samfund.
I geometrien betegner den omskrevne cirkel til en polygon en cirkel, som passerer gennem alle polygonens hjørner.
En polygon som har en omskreven cirkel, kaldes indskrivelig. Alle trekanter, alle rektangler og alle simple regulære polygoner er indskrivelige og har således en omskreven cirkel.
Men ikke alle polygoner er indskrivelige, idet en polygons hjørner ikke nødvendigvis ligger på en cirkel. Alle polygoner har derimod en entydig mindste omliggende cirkel, som er den mindste cirkel, som fuldstændigt omgiver polygonen. Den mindste omliggende cirkel til en indskrivelig polygon er ikke nødvendigvis lig med polygonens omskrevne cirkel. For eksempel har den mindste omliggende cirkel for en stumpvinklet trekant den længste side i trekanten som diameter, og den berører ikke det modstående hjørne.
Trekanter
Alle trekanter er indskrivelige, dvs. alle trekanter har en omskreven cirkel.
Det kan bevises ud fra den generelle ligning for en cirkel med centrum (a, b) og radius r i et retvinklet koordinatsystem:
Da ligningen har 3 parametre (a, b, r), er 3 punkters koordinatpar tilstrækkeligt til en bestemme en given cirkels ligning. En trekant er entydigt bestemt ud fra dens 3 hjørner, og da en cirkel kan bestemmes ud fra 3 punkter, følger at alle trekanter er indskrivelige.
Konstruktion med passer og lineal
Centrum for en trekants omskrevne cirkel kan konstrueres ved at tegne 2 ud af trekantens 3 midtnormaler. Cirklens centrum er punktet, hvor midtnormalerne skærer hinanden, og cirklens radius er afstanden fra centrum til ethvert af trekantens hjørner.
Det skyldes at den omskrevne cirkels centrum er ækvidistant (dvs. har samme afstand) til trekantens hjørner, og at alle punkter på en midtnormal er ækvidistante til 2 af trekantens hjørner.
Den omskrevne cirkels centrum i forhold til en trekant
Placeringen af den omskrevne cirkels centrum afhænger af trekantens type:
- Hvis trekanten er spidsvinklet (alle vinkler er mindre end en ret vinkel), ligger cirklens centrum inde i trekanten.
- Hvis trekanten er stumpvinklet (en vinkel er større end en ret vinkel), ligger cirklens centrum uden for trekanten.
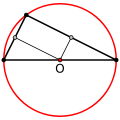
- Hvis trekanten er retvinklet, ligger cirklens centrum på midten af trekantens hypotenuse.
-
Den omskrevne cirkels centrum er inden i en spidsvinklet trekant -
Den omskrevne cirkels centrum er uden for en stumpvinklet trekant -
Den omskrevne cirkels centrum er midt på en retvinklet trekants hypotenuse
_Circumscribed.svg)
_Circumscribed.svg)
_Circumscribed.svg)
Indskrivelige firkanter
Hovedartikel: Indskrivelig firkant.Indskrivelige firkanter har særlige egenskaber, bl.a. at modstående vinkler har vinkelsummen 180° eller π radianer.